18 апреля 2024г.

Докладчик: Уртаева Александра Артуровна, Северо-Осетинский государственный университет имени К.Л. Хетагурова, г. Владикавказ, Россия.
Название доклада: О неосцилляции дифференциального уравнения четвёртого порядка на графе.

Аннотация. В докладе обсуждаются свойства решений дифференциального уравнения четвертого порядка на геометрическом графе (положительность, колеблемость, распределение нулей). Формулируются теоремы Штурма о разделении нулей решений.

Вводится понятие неосцилляции уравнения четвертого порядка на графе. Определение неосциллирующего уравнения даётся в терминах зон знакопостоянства непрерывной функции на графе. Устанавливается эквивалентность определения неосцилляции в терминах зон знакопостоянства с положительностью специальной фундаментальной системы решений уравнения. Также установлена связь неосцилляции уравнения четвертого порядка на графе и положительности функции Грина некоторых классов краевых задач четвёртого порядка на графе.

4 апреля 2024г.

Докладчик: Бутерин Сергей Александрович, Саратовский национальный исследовательский государственный университет имени Н.Г.Чернышевскогo, г. Саратов. Россия.
Название доклада: Об успокоении системы управления произвольного порядка с глобальным последействием на временном дереве.

Аннотация. Так называемые квантовые графы моделируют различные процессы в сложных системах, представимых в виде пространственных сетей, во многих областях науки и техники. Примером служат упругие струнные сетки, в узлах которых помимо условий непрерывности характерными являются условия Кирхгофа, выражающие баланс натяжений.

Однако в докладе предлагается иной взгляд на квантовые графы – как на временные сети, когда параметризующая ребра графа переменная отождествляется со временем. При этом каждая внутренняя вершина понимается, как момент разветвления процесса, дающий несколько различных сценариев дальнейшего его протекания.

Исследуется задача об успокоении системы управления, описываемой функционально-дифференциальными уравнениями произвольного порядка нейтрального типа с негладкими комплексными коэффициентами на произвольном дереве с глобальным запаздыванием. Последнее означает, что запаздывание распространяется через внутренние вершины дерева. Примечательно, что условия типа Кирхгофа возникают и здесь. А именно, им будет удовлетворять такая траектория течения процесса, которая является оптимальной с учетом сразу всех возможных сценариев. Устанавливается ее существование и единственность.

Ранее подобные задачи изучались исключительно на интервале для управляемых систем только первого порядка с постоянными либо гладкими коэффициентами. Рассматриваемый случай потребовал введения семейства специальных нелокальных квазипроизводных. В докладе также предполагается провести сравнение их с классическими квазипроизводными для обыкновенных дифференциальных операторов.

21 марта 2024г.

Докладчик: Собиров Зариф Ахмедович (Институт математики АН РУз, Узбекистан), Туремуратова Ариухан Абатбаевна (Национальный университет Узбекистана).
Название доклада: Обратная задача источника для параболического уравнения дробного порядка на метрическом графе звезде с интегральным условием переопределения.

Аннотация. В настоящей работе исследуется начально-краевая задача для параболического уравнения дробного порядка на метрическом графе звезде в пространствах Соболева. Сначала мы доказываем существование и единственность сильных решений прямой задачи с использованием функционального метода, предложенного Ладыженской и основанного на априорных оценках. Кроме того, мы рассматриваем обратную задачу на определение части правой части уравнения с интегральным условием переопределения.

Докладчик: Бондаренко Наталья Павловна, Саратовский государственный университет им. Н.Г. Чернышевского, г. Саратов, Россия.
Название доклада: Неполные обратные задачи для дифференциальных операторов на графах.

Аннотация. В статье 1946 г. Г. Борг доказал, что потенциал оператора Штурма-Лиувилля на конечном интервале однозначно восстанавливается по двум спектрам. В 1978 г. Х. Хохштадт и Б. Либерман показали, что если потенциал известен априори на половине интервала, то для его однозначного определения на другой половине достаточно одного спектра. В докладе будут рассмотрены обобщения задачи Хохштадта-Либермана на дифференциальные операторы на графах. Мы предположим, что коэффициенты дифференциальных выражений (например, потенциалов Штурма-Лиувилля) на некоторых ребрах графа известны априори, и исследуем вопрос о восстановлении коэффициентов на остальных ребрах по спектральным данным. Результаты по различным типам неполных обратных задач представлены в обзоре: Bondarenko N.P. Partial inverse Sturm-Liouville problems, Mathematics 11 (2023), no. 10, Article ID 2408. (44 p.) DOI: https://doi.org/10.3390/math11102408

Докладчик: Мироненко Фома Дмитриевич, Санкт-Петербургский государственный университет, г. Санкт-Петербург, Россия.
Название доклада: Принцип максимума Александрова—Бакельмана для эллиптических операторов на стратифицированном множестве типа “книжка”.

Аннотация. Доклад посвящён одному из наиболее красивых геометрических подходов к доказательству качественных свойств уравнений в частных производных — принципу максимума Александрова—Бакельмана. Отправной точкой для нашей задачи является локальная задача Вентцеля на единичном полушаре в R^n, для которой доказательство принципа максимума хорошо известно. Мы обобщим данный результат на случай стратифицированного множества вида “книжка”, представляющего из себя K единичных полушаров, вложенных в R^{n+1} и склеенных по общей плоской границе.

Докладчик: Prof. Pavel Exner, Doppler Institute for Mathematical Physics and Applied Mathematics, Prague.
Название доклада: Effects of time-reversal invariance violation in quantum graphs.

Аннотация. The topic of this talk are quantum graphs with the vertex coupling which does not preserve the time-reversal invariance. As a case study the simplest example with the asymmetry being maximal at a fixed energy will be analyzed. In this situation the high-energy scattering depends crucially on the vertex parity; we will demonstrate implications of this fact for spectral and transport properties in several classes of graphs, both finite and infinite periodic ones. In particular, we prove the Band-Berkolaiko universality for kagome lattices with this coupling. Furthermore, we discuss other time-asymmetric graphs and identify a class of such couplings which exhibits a nontrivial PT-symmetry despite being self-adjoint; we also illustrate the role of the Dirichlet component in the vertex coupling. Finally, we show how a square lattice with such a coupling behaves in the presence of a magnetic field when the two time-asymmetry effects compete. The results come from a common work with Marzieh Baradaran, Jiří Lipovský, and Miloš Tater.

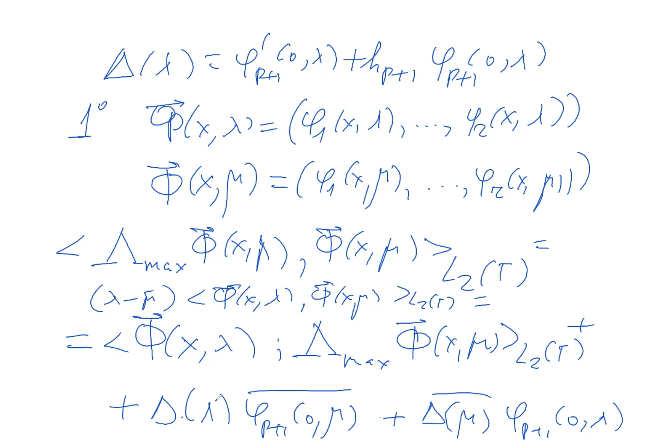Докладчик: Кангужин Баталбек Есматович, профессор кафедры математики Казахского Национального университета имени Аль-Фараби Казахстан. г. Алматы. проспект Аль -Фараби 71.
Название доклада: Критерий Вайнштейна для оператора Штурма-Лиувилля на граф-дереве и восстановление коэффициентов жесткости по конечному набору собственных значений.

Аннотация. Исследуется спектр оператора Штурма-Лиувилля на компактном граф-дереве, условия сопряжения которого содержат некоторые параметры. Их интерпретируем как коэффициенты жесткости. В исходном варианте условия сопряжения во внутренних вершинах соответствуют условиям Киргхофа. Затем последовательно изменяются условия сопряжения Киргхофа на условия сопряжения с коэффициентом жесткости. Оказывается, что собственные значения измененной задачи и исходной перемежаются. В этом заключается критерий Вайнштейна для оператора Штурма-Лиувилля на граф-дереве. В заключительной части показано, что для однозначного восстановления коэффициентов жесткости достаточно задать конечное число собственных значений некоторых родственных задач.

Докладчик: Махрова Елена Николаевна, доцент кафедры дифференциальных уравнений, математического и численного анализа Нижегородского государственного университета им. Н.И. Лобачевского.
Название доклада: Топологическая энтропия и динамические свойства непрерывных отображений на одномерных разветвленных континуумах.

Аннотация. В настоящее время наблюдается интенсивное развитие теории динамических систем на одномерных разветвленных континуумах. Это связано с тем, что одномерные разветвленные континуумы появляются, например, как множества Жюлиа в комплексных динамических системах (Х.-О. Пайтген, П. Рихтер), как предельные множества некоторых динамических систем (Ф. Балибре), как глобальный аттрактор косого произведения (Л.С. Ефремова), в задачах математической физики (В.Ж. Сакбаев, О.Г. Смолянов, А.И. Шафаревич, А.В. Цветкова), в теории ветвящихся случайных блужданий (Е.В. Булинская); отображение на конечном графе имитирует поведение гладкого потока на многообразии в окрестности гиперболического аттрактора (R.F. Williams).

В докладе изучаются достаточные условия положительности топологической энтропии непрерывных отображений на одномерных разветвленных континуумах. Будут представлены критерии простоты/сложности непрерывных отображений на определенном классе указанных континуумов. В докладе также будут представлены различия в энтропийных свойствах отображений, заданных на отрезках, конечных деревьях и на одномерных континуумах со сложной топологической структурой.

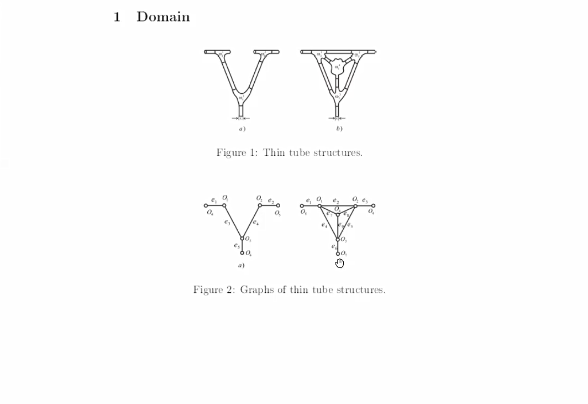Докладчик: Панасенко Григорий Петрович, University Jean Monnet, Saint-Etienne, France.
Название доклада: Задачи на графах, возникающие при асимптотическом анализе уравнений движения вязкой жидкости в трубчатой структуре.

Аннотация. Трубчатые структуры — объединения пересекающихся тонких цилиндров — часто рассматриваются как геометрические модели сети кровеносных сосудов или частей гидротехнических сооружений. Такие области содержат малый параметр: отношение порядка диаметра цилиндра к его высоте. Если формально положить диаметры цилиндров равными нулю, область вырождается в геометрический граф. Асимптотический анализ моделей течения вязкой жидкости в этих областях приводит к стационарным эллиптическим или нестационарным нелокальным по времени задачам на графе структуры. В докладе будут рассмотрены эти задачи и приведены теоремы существования и единственности решения.

09 ноября 2023г.

Докладчик: Юрко Вячеслав Анатольевич, Саратовский национальный исследовательский государственный университет имени Н.Г.Чернышевского, Саратов, Россия.
Название доклада: Дифференциальные операторы с неинтегрируемыми особенностями. Обоснование метода Фурье.
Аннотация. Будет дан краткий обзор основных результатов и методов спектральной теории дифференциальных операторов с неинтегрируемыми особенностями. Будет также обсужден вопрос об обосновании метода Фурье.

02 ноября 2023г.

Докладчик: Прядиев Владимир Леонидович, Воронежский государственный университет, Воронеж, Россия.
Название доклада: Метод граничных режимов для волнового уравнения на геометрическом графе (продолжение).
Аннотация. Поведение решения волнового уравнения в вершинах геометрического графа можно истолковать как граничные режимы по отношению к рёбрам геометрического графа. В итоге описание поведения решения на рёбрах приводит к необходимости решать векторное (по количеству вершин) дифференциально-разностное уравнение нейтрального типа на полуоси, правда, с неограниченным ростом количества запаздываний при неограниченном росте аргумента. В некоторых частных случаях решение последнего уравнения можно представить в конечном виде. В докладе предполагается подробно остановиться на технике, приводящей к ключевым соотношениям и формулам.

26 октября 2023г.

Докладчик: Прядиев Владимир Леонидович, Воронежский государственный университет, Воронеж, Россия.
Название доклада: Метод граничных режимов для волнового уравнения на геометрическом графе.
Аннотация. Поведение решения волнового уравнения в вершинах геометрического графа можно истолковать как граничные режимы по отношению к рёбрам геометрического графа. В итоге описание поведения решения на рёбрах приводит к необходимости решать векторное (по количеству вершин) дифференциально-разностное уравнение нейтрального типа на полуоси, правда, с неограниченным ростом количества запаздываний при неограниченном росте аргумента. В некоторых частных случаях решение последнего уравнения можно представить в конечном виде. В докладе предполагается подробно остановиться на технике, приводящей к ключевым соотношениям и формулам.

12 октября 2023г.

Докладчик: Назаров Александр Ильич (совм. с К.М. Медведевым), Санкт-Петербургский государственный университет, ПОМИ РАН им. В.А. Стеклова, Санкт-Петербург, Россия.
Название доклада: Оценка Гельдера для решения дивергентного эллиптического уравнения на стратифицированном множестве.
Аннотация. В докладе рассматривается равномерно эллиптическое уравнение второго порядка дивергентного типа на стратифицированном множестве. Даются априорные оценки решений.

Препринт доступен по адресу http://www.mathsoc.spb.ru/preprint/2023/23-02.pdf

28 сентября 2023г.

Докладчик: Даирбеков Нурлан Слямханович, Пенкин Олег Михайлович, Савастеев Денис Владимирович.
Название доклада: Метод Перрона в задаче Дирихле для мягкого лапласиана.
Аннотация. В докладе будет дано обобщение классического метода Перрона доказательства разрешимости задачи Дирихле на случай мягкого лапласиана на стратифицированном множестве. Будут обсуждены неравенство Харнака и теорема о стирании особенностей, играющие ключевую роль для реализации метода Перрона в рассматриваемой ситуации. Будет также предложен метод построения барьеров для мягкого лапласиана на стратифицированном множестве.

2022-2023

27 апреля 2023г.

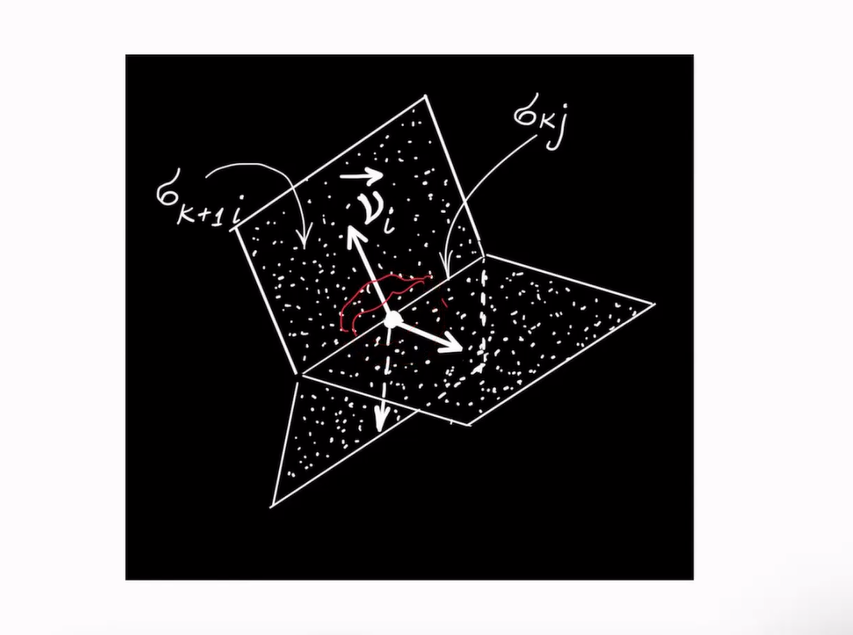Докладчик: Даирбеков Нурлан Слямханович, Национальный исследовательский технический университет имени К. И. Сатпаева, Казахстан.
Название доклада: Гармонические функции на стратифицированном множестве.
Аннотация. В докладе будет обсуждаться теорема об устранимых особенностях гармонических функций на стратифицированном множестве.

20 апреля 2023г.

Докладчик: Собиров Зариф Ахмедович, Национальный университет Узбекистана имени М. Улугбека, Ташкент, Узбекистан.
Название доклада: Метод Фокаса (унифицированного преобразования) для уравнения теплопроводности на метрических графах.
Аннотация. Обобщается метод унифицированного преобразования Фокаса для решения уравнения теплопроводности на случай некоторых простых метрических графов. Основной целью доклада является демонстрация преимущества и простоты использования вышеуказанного метода для решения начально-краевых задач на метрических графах.

13 апреля 2023г.

Докладчик: Каплун Александр Владимирович (совместно с М.И. Белишевым), Санкт-Петербургское отделение Математического института им. В.А. Стеклова РАН, Санкт-Петербург, Россия.
Название доклада: Алгебра эйконалов метрического графа: мотивация использования в обратной задаче и текущие результаты.
Аннотация. Доклад состоит из двух частей. Первая будет посвящена краткому изложению теории C*-алгебр и основных результатов, которые используются в работе, а также определению и описанию результатов, связанных с алгеброй эйконалов в простом случае риманова многообразия с краем. Вторая часть будет посвящена непосредственному описанию задачи на графе. Будут рассмотрены сходства и различия с первой задачей, а также будет сформулирован основной результат — восстановление по данным обратной задачи (спектральным или динамическим) некоторого графа, напрямую связанного с исходным. Подробно представленные результаты изложены в статье [1].

1. M. I. Belishev, A. V. Kaplun, “Canonical forms of metric graph eikonal algebra and graph geometry”, Zap. Nauchn. Sem. POMI, vol. 519, 35-66, St. Petersburg, 2022 http://www.pdmi.ras.ru/znsl/2022/v519/abs035.html, arXiv: https://arxiv.org/abs/2210.13246

06 апреля 2023г.

Докладчик: Борисов Денис Иванович, Институт математики с вычислительным центром УФИЦ РАН, Уфа, Россия.
Название доклада: О резольвентах операторов на графах с малыми ребрами.
Аннотация. В докладе обсуждается модель графа общего вида, часть ребер которого малы. Длины малых ребер характеризуются малым параметром. На таком графе рассматривается общий эллиптический оператор второго порядка и исследуется поведение его резольвенты при уменьшении малого параметра. Показывается, что резольвента раскладывается в прямую сумму двух операторов, каждый из которых в подходящем смысле аналитичен по малому параметру. Предъявляется рекуррентный алгоритм, который позволяет определить коэффициенты рядов Тейлора для каждого из этих двух операторов, что в итоге дает представление для исходной резольвенты в виде сходящего ряда типа Тейлора с рекуррентно определяемыми коэффициентами.

30 марта 2023г.

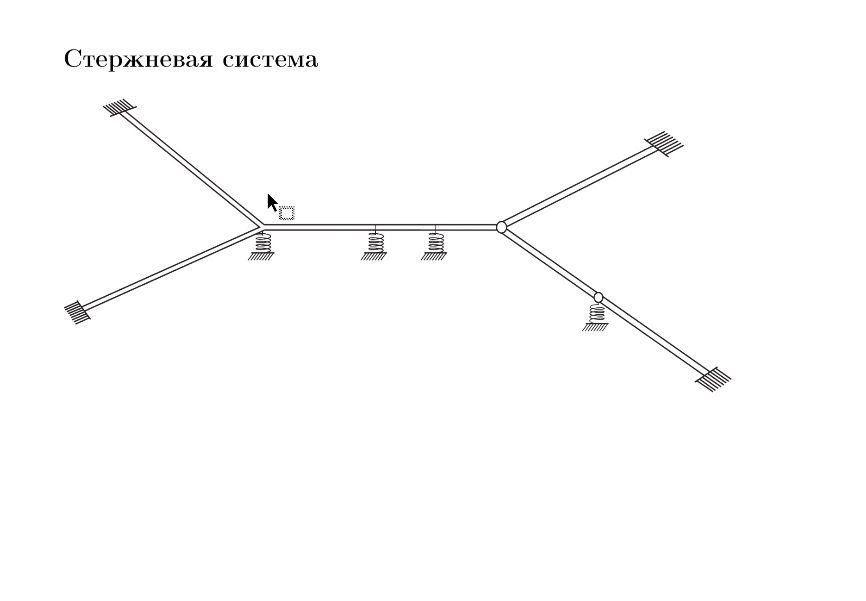Докладчик: Кулаев Руслан Черменович, Южный математический институт ВНЦ РАН, Владикавказ, Россия.
Название доклада: О положительности функции Грина краевой задачи 4-го порядка на графе.
Аннотация. В докладе будет рассмотрена краевая задача, возникающая при моделировании малых деформаций плоской стержневой системы. В узлах задаются условия жесткой спайки стержней. Обсуждается вопрос об условиях однозначной разрешимости краевой задачи и условиях положительности соответствующей функции Грина.

23 марта 2023г.

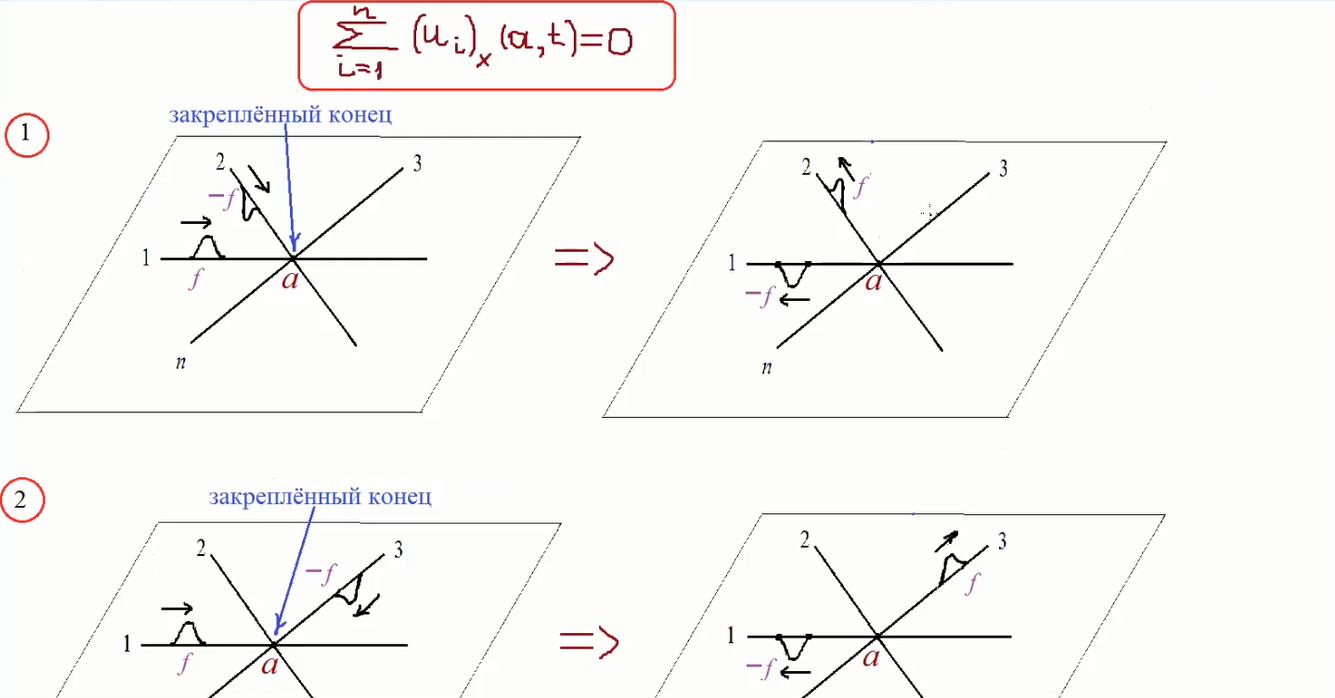Докладчик: Прядиев Владимир Леонидович, Воронежский государственный университет, Воронеж, Россия.
Название доклада: Различные представления решений начально-краевых задач для волнового уравнения на геометрическом графе.
Аннотация. В докладе предполагается изложить три подхода к описанию решений начально-краевых задач для волнового уравнения на геометрическом графе. Метод Фурье рассматриваться не будет. Один из подходов приводит к аналогу формулы Даламбера, другой даёт интегральное представление решения с ядром, выражаемым через решение системы линейных недифференциальных уравнений с постоянными запаздываниями. Третий подход, апробированный для нескольких классов условий трансмиссии, основан на трактовке функций u(v,t), где v пробегает набор внутренних вершин, как граничных режимов по отношению к примыкающим рёбрам.

16 марта 2023г.

Докладчик: Зверева Маргарита Борисовна, Воронежский государственный университет, Воронеж, Россия.
Название доклада: О математических моделях упругих систем с нелинейным условием.
Аннотация. В докладе будет рассмотрена модель деформаций струнной системы, расположенной вдоль геометрического графа-звезды, с нелинейным условием в узле. Такого рода условие возникает за счет установленного в узле ограничителя на перемещение из состояния равновесия. Отклонение изучаемой физической системы от положения равновесия описывается с помощью интегро — дифференциальных уравнений с интегралами Стилтьеса, что позволяет учитывать локализованные в отдельных точках ребер особенности (сосредоточенные силы, упругие опоры) и проводить поточечный анализ как решений, так и соотношений. Кроме того, будет рассмотрен ряд моделей колебаний струнных систем в предположении, что ограничитель может двигаться в перпендикулярном направлении к плоскости, в которой расположена исследуемая струнная система в положении равновесия.

9 марта 2023г.

Докладчик: Бондаренко Наталья Павловна, Саратовский государственный университет имени Н.Г. Чернышевского, Саратов, Россия.
Название доклада: Характеризация спектральных данных оператора Штурма-Лиувилля на графе-звезде.
Аннотация. Доклад посвящен обратной спектральной задаче, которая состоит в восстановлении коэффициентов оператора Штурма-Лиувилля на графе-звезде по спектральным данным. Решение задачи основано на представлении оператора в матричной форме и на развитии идей метода спектральных отображений — наиболее универсального метода в теории обратных спектральных задач. Получены необходимые и достаточные условия разрешимости обратной задачи, иными словами, дана характеризация спектральных данных рассматриваемого оператора. Доклад основан на результатах статьи [1] и ряда предшествующих работ автора.

2 марта 2023г.

Докладчик: Лазарев Константин Петрович, Воронежский государственный университет, Воронеж, Россия.
Название доклада: Краевые задачи для неосциллирующих дифференциальных операторов.
Аннотация. Рассматриваются некоторые классы многоточечных краевых условий, для которых краевая задача с неосциллирующим дифференциальным оператором однозначно разрешима. В некоторых случаях рассмотрены спектральные задачи.

16 февраля 2023г.

Докладчик: Бурлуцкая Мария Шаукатовна, Воронежский государственный университет, Воронеж, Россия.
Название доклада: О некоторых спектральных вопросах для функционально-дифференциальных и интегральных операторов на геометрическом графе и новых подходах в решении смешанных задач.
Аннотация. В первой части доклада будут представлены исследования некоторых спектральных свойств функционально-дифференциальных операторов с инволюцией на графе, и их приложений в решении смешанных задач. Вторая часть посвящена новым подходам в методе Фурье и их применению в задаче для волнового уравнения на графе.

9 февраля 2023г.

Докладчик: Эфендиев Ракиб Фейруз оглы, Бакинский Инженерный Университет, Баку, Азербайджан.
Название доклада: Спектральный анализ одного класса несамосопряженных обыкновенных дифференциальных операторов с периодическими коэффициентами на графах.
Аннотация. Рассматривается спектральный анализ распространения волны в слоистой, неоднородной среде, таких как ветвящаяся трубка или система соединённых струн. С этой целью на звёздном графе исследуется задача распространения волн в одномерной неконсервативной среде в частотной области.

2 февраля 2023г.

Докладчик: Шафаревич Андрей Игоревич, Московский государственный университет имени М.В. Ломоносова, Москва, Россия.
Название доклада: Локализованные асимптотические решения эволюционных уравнений на графах и сингулярных пространствах. Связь с поведением геодезических и задачами аналитической теорией чисел.
Аннотация. Описаны асимптотические решения задачи Коши для эволюционного уравнения (Шредингера или волнового) на геометрическом графе и сингулярном пространстве, полученном из графа заменой вершин на римановы многообразия. Начальные условия выбираются в виде гауссова пакета, локализованного вблизи точки ребра. Описано поведение пакета при прохождении вершины или точки склейки и изучена статистика асимптотических носителей решения. Показано, что эта статистика связана с поведением геодезических на многообразиях и с некоторыми задачами аналитической теории чисел.

8 декабря 2022г.

Докладчик: Дедок Василий Александрович, Институт математики им. С.Л. Соболева СО РАН, Новосибирский национальный исследовательский государственный университет, Новосибирск, Россия.
Название доклада: Дифференциальные уравнения на геометрических графах.
Аннотация. В докладе рассматриваются прямые и обратные задачи для дифференциальных уравнений на геометрических графах. В частности, исследуются свойства решений для уравнения Шредингера и данные рассеяния на таких объектах. Прямые задачи посвящены конструированию данных рассеяния при сборке сложных графов из более простых подграфов. Обратные задачи связаны с восстановлением топологической и метрической структуры графа по данным рассеяния оператора Шредингера на нем. В завершение доклада приводится связь моделей дифференциальных уравнений и квантового случайного блуждания.

1 декабря 2022г.

Докладчик: Зимин Решат Нариманович, Satbayev University, Алматы, Казахстан.
Название доклада: О близости низкочастотных частей спектров колебаний мембран и сеток из струн.
Аннотация. Доклад посвящен обзору некоторых подходов к исследованию низкочастотных частей спектров непрерывных механических сред (мембран, пластин) и аналогичной части спектра полунепрерывных сред (сеток из струн или стержней).

24 ноября 2022г.

Докладчик: Александр Ильич Назаров, Санкт-Петербургское отделение Математического института им. В. А. Стеклова РАН, Санкт-Петербургский государственный университет, Санкт-Петербург.
Название доклада: Повторные потенциалы для уравнений Лапласа и Гельмгольца.
Аннотация. Доклад посвящен исследованию задачи Вентцеля для уравнений Лапласа и Гельмгольца в ограниченной области с границей класса C2 . Для решения этой задачи (и некоторых более сложных задач математической физики) вводятся повторные потенциалы и устанавливается существование нормальных производных.

17 ноября 2022г.

Докладчик: Елена Николаевна Махрова, Институт информационных технологий, математики и механики ННГУ им. Н.И. Лобачевского, Нижний Новгород.
Название доклада: Структура дендритов и динамика непрерывных отображений на них.
Аннотация. Доклад посвящен исследованию непрерывных отображений на одномерных континуумах, которые допускают бесконечное число точек ветвления бесконечного порядка (дендриты, локальные дендриты и дендроиды). Подобные одномерные континуумы со сложной топологической структурой появляются, например, как множества Жюлиа (Х.-О. Пайтген, П. Рихтер), как предельные множества некоторых динамических систем (Ф. Балибре), как глобальный аттрактор косого произведения (Л.С. Ефремова), а также в задачах математической физики (В.Ж. Сакбаев, О.Г. Смолянов, А.И. Шаваревич, А.В. Цветкова).

Работы по изучению отображений на одномерных континуумах со сложной топологической структурой показали принципиальные различия в динамике указанных отображений и отображений отрезка, окружности, конечных деревьев и конечных графов (Л.С. Ефремова, Е.Н. Махрова, Дж. Каратоник, и др.).

В докладе будут представлены указанные различия в динамике даже простейших монотонных отображений на дендритах (локально связных континуумах, не содержащих подмножеств, гомеоморфных окружности); продемонстрирована зависимость некоторых динамических свойств непрерывных отображений дендритов от структуры самого дендрита.

10 ноября 2022г.

Докладчик: Тедеев Анатолий Федорович, Владикавказский научный центр РАН, Юго-Осетинский государственный университет им. А.А. Тибилова, Цхинвал.
Название доклада: Асимптотические оценки для р-Лапласиана на бесконечных графах с начальными данными убывающих на бесконечности.
Аннотация. Целью доклада является исследование поведения решения задачи Коши для нестационарного параболического уравнения типа р-Лапласиана на бесконечных весовых графах, геометрия которых описывается в терминах неравенств типа Фабэра-Крана. Дается точная оценка скорости стабилизации решения решения в зависимости от поведения начальной функции.

3 ноября 2022г.

Докладчик: Даирбеков Нурлан Салямханович, Национальный исследовательский технический университет имени К. И. Сатпаева, Казахстан.
Название доклада: Неравенства Пуанкаре и Соболева на стратифицированных множествах.
Аннотация. Рассматриваются аналоги упомянутых неравенств и их приложения к р-лапласиану на стратифицированных множествах.

27 октября 2022г.

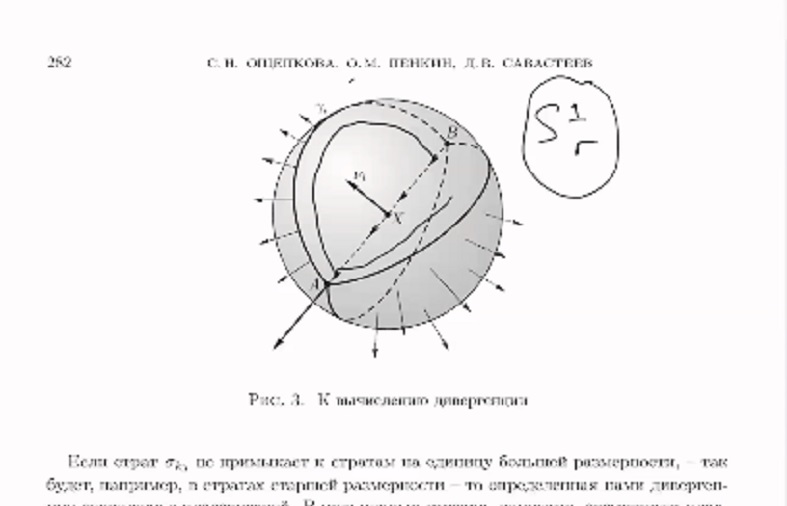Докладчик: Пенкин Олег Михайлович, Воронежский государственный университет, Воронеж, Россия.
Название доклада: О сильном принципе максимума для субгармонических функций на стратифицированном множестве.
Аннотация. Будет сформулирован сильный принцип максимума для субгармонических функций, заданных на стратифицированном множестве.

20 октября 2022г.

Докладчик: Кулаев Руслан Черменович, Владикавказский научный центр РАН, Северо-Осетинский госуниверситет, Владикавказ, Россия.
Название доклада: Краевые задачи четвертого порядка на графах.
Аннотация. Будут представлены краевые задачи, возникающие при моделировании стержневых конструкций. Описываются постановки краевых задач четвёртого порядка на графах и, в частности, условия согласования в узловых вершинах графа. Будет дан краткий обзор результатов, связанных с дифференциальными уравнениями четвёртого порядка на сетях.

13 октября 2022г.

Докладчик: Юрко Вячеслав Анатольевич, Национальный исследовательский Саратовский государственный университет имени Н.Г. Чернышевского, Саратов, Россия.
Название доклада: Обратные спектральные задачи для дифференциальных операторов на графах.
Аннотация. Будет дан краткий обзор по теории обратных спектральных задач для
обыкновенных дифференциальных операторов, заданных на геометрических графах.
Основное внимание будет уделено обратным задачам, в которых структура графа
предполагается известной и фиксированной, и задача заключается в восстановлении
коэффициентов операторов по заданным спектральным характеристикам.
При этом будут рассмотрены как простейшие операторы, а именно, операторы
Штурма-Лиувилля, так и более сложные операторы высших порядков, а также
операторы переменных порядков.

06 октября 2022г.

Докладчик: Сакбаев Всеволод Жанович, ИПМ им. М.В. Келдыша РАН, Москва, Россия.
Название доклада: Композиции независимых случайных операторов и связанные с ними дифференциальные уравнения.
Аннотация. Исследуются итерации независимых случайных линейных операторов, действующих в гильбертовом пространстве квадратично интегрируемых функций на евклидовом пространстве. Рассматриваемые случайные операторы принимают значение в алгебре операторов, порожденной операторами аффинного преобразования аргумента функции либо ее Фурье-образа. Получены условия, достаточные для сходимости последовательности математических ожиданий композиций операторнозначных процессов со значениями в рассматриваемой алгебре операторов к полугруппам, описывающим диффузию в евклидовом пространстве. Описаны генераторы предельных полугрупп.

29 сентября 2022г.

Докладчик: Пенкин Олег Михайлович, Воронежский государственный университет, Воронеж, Россия.
Название доклада: Об эллиптических уравнениях на стратифицированных множеств.
Аннотация. Будут затронуты следующие вопросы:
1. История вопроса (начиная с Р. Куранта).
2. Как правильно формализовать уравнение на стратифицированном множестве.
3. Некоторые результаты о качественном поведении решений эллиптических уравнений на стратифицированном множестве, объединяющие известные классические результаты, ранее казавшиеся самостоятельными. Здесь мы дадим первую попытку убедить участников семинара, что Бог создал задачу Дирихле, всё остальное — дело рук человеческих.
4. Мы обсудим интересные связи между разрешимостью задачи Дирихле (для стратифицированного лапласиана и p-лапласиана) и геометрическим устройством стратифицированного множества, на котором она ставится.
В докладе не будет обсуждаться техника получения результатов, хотя она довольно красива и поучительна. Мы надеемся, что детальные доклады будут сделаны людьми, хорошо ориентирующимися в данной проблематике.

22 сентября 2022г.

Докладчик: Прядиев Владимир Леонидович, Воронежский государственный университет, Воронеж, Россия.
Название доклада: Теория Штурма для линейного дифференциального уравнения на геометрическом графе. Кратность собственных значений задачи Штурма-Лиувилля на графе.
Аннотация. Доклад, имеющий обзорный характер, посвящен осцилляционной спектральной теории – распределению нулей в задаче Штурма – Лиувилля на пространственных сетях (геометрических графах).

15 сентября 2022 г.

Докладчик: Боровских Алексей Владиславович, Московский государственный университет имени М.В. Ломоносова, Москва, Россия.
Название доклада: Теория дифференциальных уравнений на графах: феноменология и проблемное поле.
Аннотация. В докладе, имеющем обзорный характер, теория дифференциальных уравнений на пространственных сетях (геометрических графах) будет представлена как определённый круг уникальных для этого объекта феноменов и как некоторое проблемное поле исследований, проводимых в данной области различными исследователями, в том числе участниками семинара. Такое представление придаёт этому разделу теории дифференциальных уравнений некую целостность, а, с другой стороны, придаёт этой целостности достаточную компактность и обозримость.